Przyszła środa, a więc czas na pierwszy zbiór przykładów. Zaczniemy najprościej jak to możliwe. Wygenerujemy kilka syntetycznych zbiorów danych, zapisując je później do plików CSV.
Syntetyczne zbiory danych
Co do zasady jest tak, że w prawdziwych badaniach naukowych (takich poważnych, które podobno będzie ktoś czytać) nie powinniśmy raczej korzystać ze zbiorów syntetycznych – tj. wygenerowanych przez algorytm prób wzorców, które nie przedstawiają żadnego prawdziwego problemu.
Mimo tego, okazują się bardzo przydatne. Pozwalają nam łatwo i szybko uzyskać wiele jednocześnie różnych i powtarzalnych (kochajmy random_state) prób problemu, które spełniają postawione przez nas wymagania. Przykładowo, możemy wygenerować na raz dziesięć różniących się od siebie zbiorów danych, z których każdy będzie mieć dokładnie trzydzieści obiektów (mała liczba wzorców) mających po tysiąc atrybutów (wysoka wymiarowość problemu).
Duża część pracy badawczej, szczególnie na początku każdych badań, to budowanie prototypów – pierwszych podejść do problemów, które powinniśmy być w stanie szybko przetestować, żeby wcześnie wyłapać błędy programistyczne i koncepcyjne wymyślonej przez nas metody. Dzięki temu znacznie szybciej uda się przejść z etapu prototypowania do konstrukcji gotowego już algorytmu, który oczywiście na koniec przetestujemy już na zbiorach rzeczywistych.
Generowanie zbiorów syntetycznych
Dosyć przekonywania, że to przydatne, przejdźmy do przykładu.
from sklearn import datasets
X, y = datasets.make_classification()
W pierwszej linijce przykładu, z biblioteki scikit-learn importujemy moduł datasets, odpowiadający m.in. za wczytywanie kilku standardowych zbiorów danych (niektóre mają po sto lat, więc przez jakiś czas nie będziemy się nimi raczej przejmować) i właśnie za generowanie zbiorów syntetycznych. Służy do tego funkcja make_classification(), którą wywołaliśmy na końcu tego krótkiego przykładu. Zwraca ona krotkę (X, y), której pierwszy element to – zgodnie z oznaczeniami, które już raczej znamy – zbiór danych, a drugi jest zbiorem etykiet. Podejrzyjmy jakiej wielkości struktury są generowane przez nią domyślnie
print(X.shape, y.shape)
>> (100, 20) (100,)
W zbiorze danych (macierz X) znajduje się sto wierszy po dwadzieścia elementów. Oznacza to, że wygenerowaliśmy sto wzorców, każdy po dwadzieścia atrybutów. W zbiorze etykiet znajdują się (szokujące) etykiety dla każdego ze wzorców.
Argumenty funkcji make_classification()
Oczywiście, każdy z tych parametrów możemy kontrolować. Przykładowo, wygenerujmy zbiór danych zawierający tysiąc ośmiowymiarowych wzorców.
X, y = datasets.make_classification(n_samples=1000, n_features=8)
print(X.shape, y.shape)
>> (1000, 8) (1000,)
Kolejne parametry (n_samples, n_features) przekazujemy jako argumenty funkcji. Zaimplementowana w niej metoda (oryginalnie służąca do generowania zbioru Madelon i opracowana w 2003. roku przez Panią Isabelle Guyon) przyjmuje wiele argumentów, ale wymienimy sobie z nich tylko te, które okażą nam się najbardziej przydatne w eksperymentach na potrzeby laboratorium i projektu (jeśli kiedykolwiek jeszcze się na nich spotkamy):
n_samples— liczba generowanych wzorców (domyślnie 100).n_features— liczba atrybutów zbioru (domyślnie 20).n_classes— liczba klas problemu (domyślnie 2, a więc problem binarny).n_clusters_per_class— liczba centroidów dla każdej klasy, a więc liczba skupisk każdej z klas problemu (domyślnie 2).flip_y— poziom szumu, a więc liczba etykiet, które celowo mają posiadać błędne przypisanie (domyślnie 0.01).random_state— ziarno losowości, które pozwala na wygenerowanie dokładnie tego samego zbioru w każdym powtórzeniu skryptu (domyślnie None, czyli losowe ziarno losowości).
Poza tymi podstawowymi własnościami zbioru danych, na początek warto jeszcze dowiedzieć się jak sterować rodzajami generowanych atrybutów. W wypadku tego generatora wszystkie cechy będą ilościowymi, ale możemy modyfikować charakterystykę ich przydatności w budowie modelu. Istotne argumenty w tym wypadku to:
n_informative— liczba atrybutów informatywnych, a więc tych, które faktycznie zawierają informacje przydatne dla klasyfikacji, a nie jedynie szum (domyślnie 2).n_redundant— liczba atrybutów nadmiarowych, będących kombinacjami cech informatywnych (domyślnie 2).n_repeated— liczba atrybutów powtórzonych, czyli zduplikowanych kolumn, losowo wybranych z informatywnych i redundantnych (domyślnie 2).
Domyślnie zatem generowany jest niepowtarzalny (brak ziarna losowości) binarny problem, który składa się ze stu wzorców, a jedynie sześć z jego dwudziestu atrybutów zawiera informacje potencjalnie przydatne (dwa informatywne, dwa to kombinacje informatywnych i dwa powtarzają losowe z czterech poprzednich), a reszta składa się wyłącznie z szumu.
Wymyślamy problem
Uzbrojeni w wiedzę o parametrach make_classification() możemy wymyślić sobie problem. Niech będzie to odtwarzalny (ziarno 1410), dwuwymiarowy zbiór danych, w którym jedynie jeden atrybut będzie informatywny (w drugim znajdzie się szum) i składa się ze stu wzorców o poziomie szumu wynoszącym pięć procent dla problemu binarnego.
X, y = datasets.make_classification(
n_samples=100,
n_features=2,
n_informative=1,
n_repeated=0,
n_redundant=0,
flip_y=.05,
random_state=1410,
n_clusters_per_class=1
)
Dwuwymiarowy zbiór wygenerowaliśmy po to, żeby móc wygenerować jego scatterplot. Kolejno, importujemy bibliotekę matplotlib, przygotowujemy pustą ilustrację o wymiarach 5 na 2.5 cala, rysujemy scatterplot (podając osobno kolumny z wymiarami i określając kolor – c – przez wygenerowane etykiety), opisujemy osi i zapisujemy plik PNG.
import matplotlib.pyplot as plt
plt.figure(figsize=(5,2.5))
plt.scatter(X[:,0], X[:,1], c=y, cmap='bwr')
plt.xlabel("$x^1$")
plt.ylabel("$x^2$")
plt.tight_layout()
plt.savefig('sroda1.png')
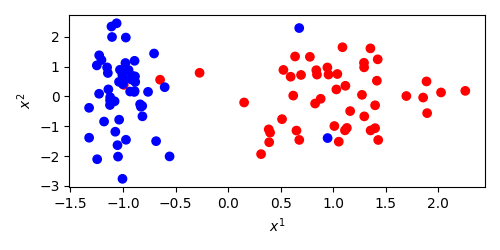
Jak widać na załączonym obrazku, pierwszy atrybut pozwala na rozróżnienie klas, a więc jest informatywny a drugi zawiera wyłącznie szum. Dodatkowo, w obu skupiskach widać pojedyncze obiekty o oryginalnie błędnej etykiecie, w sumie składające się na dokładnie pięć obiektów, a więc pięć procent z wygenerowanej setki obiektów.
Zapisujemy problem
Na koniec powtórzymy sobie coś, co pokazywałem już Państwu na początku drugiego wykładu. Zbiory danych bardzo często udostępniane są jako pliki CSV. W razie gdyby ktoś nie znał tego formatu, są to bardzo proste pliki tekstowe reprezentujące tablice, w których każdy wiersz opisuje pojedynczy rekord (w naszym wypadku wzorzec), a każdy atrybut oddzielamy od siebie separatorem w postaci przecinka.
Dodatkowym wymaganiem o którym często się zapomina jest zapewnienie w takim pliku, aby każdy wiersz miał dokładnie tyle samo elementów (a więc i tyle samo separatorów). Odmianą tego formatu jest też TSV (tab-separated values), gdzie wartości oddzielamy znakiem tabulacji. Jeśli się uprzemy, możemy wartości oddzielać dowolnym wybranym przez nas separatorem, ale nie szarżujmy, żeby na przykład używać gwiazdki czy wykrzyknika. Ani nikt tego nie zrozumie, ani na nic się to nikomu nie przyda.
W pierwszej kolejności powinniśmy połączyć ze sobą zbiór danych i zbiór etykiet, dokładając y jako dodatkową, ostatnią kolumnę macierzy X. Uznanie zbioru etykiet za ostatnią kolumnę zbioru w formie serializowanej jest czysto umowne, ale możemy założyć, że to wygodne rozwiązanie.
Przyda nam się tutaj numpy i jej wbudowana funkcja concatenate(). Jak możemy przeczytać w dokumentacji, jako pierwszy atrybut (nienazwany i pozycyjny) przyjmuje “sekwencję lub tablicę tablic o tym samym kształcie”. Sekwencję zrozumiemy jako krotkę (X, y), mimo, że moglibyśmy spokojnie przekazać tam także tablicę.
Przekazanie jej w takiej najprostszej postaci zakończy się jednak błędem wynikającym z tego, że nie zapewniliśmy naszym tablicom numpy wspólnego kształtu. Powinniśmy rozumieć go jako:
- tą samą liczbą wymiarów (długość wektora zwracaną przez atrybut
shapetablicy), - tą samą wielkością we wszystkich wymiarach poza jednym.
Nasz ostatni wygenerowany zbiór danych ma wymiary (100, 2), a zbiór etykiet (100), a więc nie spełniamy pierwszego z tych dwóch warunków. Możemy to nadrobić adresując y w sposób, który wygeneruje na jego końcu dodatkowy wymiar i zacznie traktować nie jako wektor, a jako macierz z pojedynczą kolumną. Możemy osiągnąć to przez wywołanie y[:, np.newaxis].
Drugim niezbędnym nam atrybutem funkcji concatenate() jest axis, czyli oś, w której planujemy złączyć ze sobą przekazane tablice. Powinniśmy wskazać nim w którym wymiarze (której osi) tablice mają różną wielkość. W naszym wypadku jest to drugi parametr, więc licząc od zera powinniśmy przekazać tam wartość 1. Poprawne złączenie możemy zatem zapisać jak poniżej:
import numpy as np
dataset = np.concatenate((X, y[:, np.newaxis]), axis=1)
Pojedynczą macierz możemy już bez trudu zapisać w pliku tekstowym o formacie CSV, znów korzystając z metody wbudowanej numpy savetxt().
Ma ona dwa argumenty pozycyjne. W pierwszym podajemy łańcuch z nazwą pliku, w drugim tablicę, którą chcemy zapisać. Dodatkowo, jeśli chcemy spełnić wymagania formatu CSV, powinniśmy również zmienić domyślny separator na przecinek.
np.savetxt("dataset.csv", dataset, delimiter=",")
To niby wystarczy, ale jeśli podejrzymy zawartość pliku, zobaczymy, że nie wygląda najpiękniej.
-1.060890925868820389e+00,2.455805509796364028e+00,0.000000000000000000e+00
-6.853148372231210317e-01,-1.500489680108889390e+00,0.000000000000000000e+00
7.775378070067257008e-01,1.330505069088626868e+00,1.000000000000000000e+00
6.933842893245101280e-01,7.217146432694194758e-01,1.000000000000000000e+00
-2.715820952605125793e-01,7.934501868603156538e-01,1.000000000000000000e+00
Jeśli ktoś jest miłośnikiem notacji naukowej, oczywiście może zostawić to w takiej formie, ale należy szczerze przyznać, że zapis etykiety, która w końcu jest liczbą całkowitą z przepastnego, dyskretnego zbioru zawierającego jedynie zero i jedynkę, jako liczbę w notacji matematycznej z dokładnością do osiemnastu miejsce po przecinku, jest cokolwiek karkołomne. Możemy naprawić to przez ręczne podanie formatu liczb. Nie będę tego dokładnie teraz wyjaśniać, ale proszę uwierzyć, działa.
np.savetxt(
"dataset.csv",
dataset,
delimiter=",",
fmt=["%.5f" for i in range(X.shape[1])] + ["%i"],
)
-1.06089,2.45581,0
-0.68531,-1.50049,0
0.77754,1.33051,1
0.69338,0.72171,1
-0.27158,0.79345,1
Od razu lepiej, prawda?
Wracamy do problemu
No dobrze, to na koniec zobaczmy, jak wczytywać pliki CSV do tablic numpy. Znów, mamy od tego funkcję wbudowaną, nazywaną genfromtxt(). Wczytajmy zatem plik do zmiennej dataset (pamiętając o separatorze) i spójrzmy jak pięknie się wczytał.
dataset = np.genfromtxt("dataset.csv", delimiter=",")
print(dataset)
>> [[-1.06089 2.45581 0. ]
>> [-0.68531 -1.50049 0. ]
>> [ 0.77754 1.33051 1. ]
>> [ 0.69338 0.72171 1. ]
>> [-0.27158 0.79345 1. ]
...
Skoro już się wczytał, to podzielmy go jeszcze na X i y, do pierwszego przypisując wszystkie kolumny poza ostanią, a do drugiego jedynie ostatnią. Skoro etykiety są i tak liczbami całkowitymi, zrzutujmy ją przy okazji na całkowitą.
X = dataset[:, :-1]
y = dataset[:, -1].astype(int)
Pięknie. Potrafimy już zrealizować tak zaawansowane zadania jak wymyślenie problemu i zapisanie go na później, żeby zawsze móc do niego wrócić. Wybornie.
Do przeczytania w piątek!