Minął tydzień, więc powracamy z przykładami. O ile się nie mylę, to jest to czwarty zestaw od końca i zajmiemy się w nim implementacją prostego (chociaż w sumie kto wie) klasyfikatora zgodnego z API scikit-learn.

Klasyfikator najbliższych centroidów (ang. Nearest Centroid Classifier (NC))

Żeby nikogo bardzo nie przestraszyć, weźmiemy na tapet klasyfikator najbliższych centroidów. Koncepcyjnie jest on wręcz banalny, a jego działanie można przedstawić następująco:

1. Dzielimy dane treningowe na osobne klasy.
2. Wyznaczamy centroid każdej klasy problemu.
3. Dla każdej instancji z zestawu testowego, obliczamy jej odległość (wedle zadanej wcześniej miary) do każdego z centroidów.
4. Przyporządkowujemy klasyfikowaną instancję do tej klasy, której centroid znajduje się najbliżej.

Mała modyfikacja zawierająca element optymalizacji

Żeby jednak w dzisiejszym przykładzie pojawiło się jakieś wyzwanie, to do powyższego modelu dodamy opcjonalną optymalizację. Optymalizacja ta będzie polegała na wykorzystaniu reguły trzech sigm (znanej z wykładu) do pozbycia się z każdej z klas obserwacji, które nie mieszczą się w granicy 3 odchyleń standardowych od średniej. Po każdej redukcji będziemy ponownie wyznaczać centroid klasy i kolejny raz sprawdzać, czy znajdują się w niej obserwacje odstające (ang. outliers) – proces będzie powtarzany tak długo, aż wszystkie instancje klasy nie będą przekraczać rzeczonej granicy.

Procedurę tą możemy przedstawić w następujących krokach dla każdej z klas:

1. Wyznaczamy centroid klasy.
2. Wyznaczamy odchylenie standardowe wszystkich instancji klasy.
3. Wyznaczamy punkt graniczny w przestrzeni cech i odległość do granicy.
4. Uznajemy za obserwacje odstające wszystkie te, które znajdują się za wyznaczoną granicą i pozbywamy się ich.
5. Wracamy do punktu 1. i powtarzamy cały proces tak długo, dopóki będziemy w stanie wykryć kolejne outliery.

Ale starczy już tej teorii, zabierzmy się za kod.

Implementacja własnego estymatora scikit-learn

Zaimplementujemy teraz nasz klasyfikator, przechodząc po kolei przez każdą z aż trzech potrzebnych nam metod (a w sumie to inicjalizatora i dwóch metod). Dla szczególnie spragnionych wiedzy – w dokumentacji można znaleźć dodatkowe informacje na temat implementacji własnych modeli.

Importy i zalążek klasy

Tworzymy więc pusty plik onc.py i zaczynamy jak zwykłe od zaimportowania wszystkiego, co będzie nam potrzebne podczas pracy:

• numpy - to już klasyk.
• BaseEstimator - klasa bazowa dla wszystkich estymatorów scikit-learn, zawierająca metody get_param i set_params (chyba nie potrzebujące wyjaśnienia).
• ClassifierMixin - klasa zawierająca metodę score.
• check_X_y, check_array oraz check_is_fitted - metody służące do walidacji poprawności naszych danych treningowych i testowych oraz do sprawdzenia, czy nasz model został już wytrenowany.
• DistanceMetric - klasa pozwalająca na obliczanie dystansów parowych wedle zadanej metryki (jeżeli ktoś ma taką potrzebę, to można nawet zdefiniować własną funkcję dystansu).

import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted
from sklearn.neighbors import DistanceMetric

Następnie zaczynamy od zdefiniowania klasy naszego estymatora, która dziedziczyć będzie po BaseEstimator oraz ClassifierMixin. Dodamy też komentarz, coby wiedzieć, co w ogóle ta klasa implementuje.

class OptimizedNearestCentroid(BaseEstimator, ClassifierMixin):
    """
    Nearest Centroid Classifier optimized according to the three sigma rule.
    Klasyfikator najbliższych centroidów optymalizowany regułą trzech sigm.
    """

Inicjalizator (__init__)

Czas zastanowić się, jakie argumenty będą potrzebne naszemu klasyfikatorowi. Moim zdaniem będą to:

• metric - nazwa metryki dystansu, z której będzie korzystał estymator.
• optimize - mówiący nam o tym, czy chcemy skorzystać z domyślnej wersji NC, czy może jednak optymalizować.
• sigma - jaką wielokrotność odchylenia standardowego uznajemy za dopuszczalną.

Należy pamiętać o tym, aby każdy z argumentów miał wartość domyślną. Dzięki temu możemy potem zainicjować nasz model bez podawania argumentów.

  def __init__(self, metric='euclidean', optimize=True, sigma=3):
        self.metric = metric
        self.optimize = optimize
        self.sigma = sigma

Dopasowanie modelu do danych (fit())

Teraz najważniejsza metoda, czyli fit(). Oczywiście przekazujemy do niej nasze dane treningowe czyli X i y. Następnie przechodzimy przez standardową procedurę sprawdzenia kształtu danych, zapamiętania unikalnych klas problemu oraz przechowania X i y jako parametrów modelu:

  def fit(self, X, y):
        # czy X i y maja wlasciwy ksztalt
        X, y = check_X_y(X, y)
        # przechowanie unikalnych klas problemu
        self.classes_ = np.unique(y)
        # przechowujemy X i y
        self.X_, self.y_ = X, y

Teraz w końcu zrobimy coś, co faktycznie jest właściwe dla naszego konkretnego klasyfikatora. Inicjujemy obiekt DistanceMetric ze zdefiniowanym wcześniej dystansem self.metric, z którego chcemy korzystać przy obliczaniu odległości. Do tego przygotowujemy sobie listę self.centroids, która będzie kontenerem na wyznaczone przez nas centroidy klas i zaczynamy wcześniej opisaną procedurę już dla każdej klasy osobno:

        # przygotowujemy narzedzie do liczenia dystansow
        self.dm_ = DistanceMetric.get_metric(self.metric)
        # kontener na centroidy klas
        self.centroids_ = []
        # dla kazdej klasy
        for cl in self.classes_:
            # wybieramy tylko instancje nalezace do danej klasy
            X_class = self.X_[self.y_ == cl]

Gdyby życie było proste (a wszyscy wiemy, że nie jest), to pozostała część metody fit() wyglądałaby następująco:

            # wyliczamy centroid klasy
            class_centroid = np.mean(X_class, axis=0)
            # dodajemy wyliczony centroid do listy
            self.centroids_.append(class_centroid)
        # zwracamy klasyfikator
        return self

I w ten sposób byłoby po sprawie. Ale my chcemy móc skorzystać ze wspaniałej i niewątpliwie ogromnie ważnej procedury optymalizacji. W związku z tym zapominamy o kodzie przedstawionym wyżej i w jego miejsce wrzucamy kochaną i całkowicie nieodpowiednią nieskończoną pętlę. W pętli zaczynamy od wyliczenia centroidu klasy a potem dodajemy możliwość przerwania, jeżeli nie chcielibyśmy optymalizować naszego modelu:

            # petla
            while True:
                # wyliczamy centroid klasy
                class_centroid = np.mean(X_class, axis=0)
                # jeżeli nie optymalizujemy to kończymy
                if self.optimize == False:
                    break

Przed nami właściwa procedura parametryzacji. Zgodnie z założeniem liczymy odchylenie standardowe wszystkich instancji klasy (będzie to wektor). Następnie dodajemy pomnożone self.simga razy odchylenie do centroidu, aby wyznaczyć instancję graniczną (znajdującą się 3 odchylenia standardowe od centroidu). Dzięki temu możemy z wykorzystaniem self.dm policzyć dystans między tą instancją a centroidem, który jednocześnie jest największym dystansem jaki dopuszczamy dla obiektów klasy. Dalej liczymy dystans każdej instancji klasy od centroidu.

Funkcja np.squeeze() pozwala nam się pozbyć wszystkich wymiarów o wartości 1 (czyli tak naprawdę pustych), a np.reshape() jest konieczny ze względu na specyfikę wejść przyjmowanych przez DistanceMetric.

                # liczymy odchylenie standardowe instancji klasy
                std = np.std(X_class, axis=0)
                # możliwie najdalej znajdująca się instancje
                self.borderline_ = class_centroid + (self.sigma * std)
                # maksymalny dopuszczalny dystans
                accepted_distances = np.squeeze(self.dm_.pairwise(
                    class_centroid.reshape(1, X_class.shape[1]),
                    self.borderline_.reshape(1, X_class.shape[1])))
                # liczymy dystanse wszystkich obiektow klasy od centroidu
                distances = np.squeeze(self.dm_.pairwise(
                    class_centroid.reshape(1, X_class.shape[1]), X_class))

Teraz musimy zdecydować w jaki sposób chcemy usuwać z klasy obserwacje odstające. Moglibyśmy zrobić to np. poprzez wyznaczenie indeksów instancji z dystansami większymi niż dopuszczalne (np.argwhere) i skorzystanie z funkcji np.delete().

Zrobimy to jednak w inny (i często preferowany) sposób. Mianowicie skorzystamy z maski binarnej. Tworzymy więc macierz self.outliers_mask_ która odpowiada kształtem naszej macierzy distances i zawiera wartości True wszędzie tam, gdzie dystans przekracza dopuszczalną wartość (w przeciwnym razie mamy wartość False).

Teraz na zakończenie potrzebujemy warunku, który zakończy procedurę optymalizacji jeżeli nie znajdziemy żadnej obserwacji odstającej, lub usunie z klasy znalezione outliery. Usuwanie odbywa się poprzez pozostawienie w klasie tylko tych instancji, których dystanse nie przekraczają wyznaczonej przez nas granicy. Sposób z wykorzystaniem maski binarnej jest często wygodniejszy i szybszy niż np.delete().

                # uznajemy za outliery te instancje, ktore znajduja sie od
                # centroidu dalej niz 3 * std
                self.outliers_mask_ = np.array(distances > accepted_distances)
                # konczymy optymalizacje, jezeli nie mamy outlierow
                if np.sum(self.outliers_mask_) == 0:
                    break
                # w inym przypadku pozbywamy sie outlierow
                else:
                    X_class = X_class[self.outliers_mask_ == False]

            # dodajemy wyliczony centroid do listy
            self.centroids_.append(class_centroid)
        # zwracamy klasyfikator
        return self

Kiedy już skończymy optymalizację i wyjdziemy z pętli (lub wcale nie wykonamy optymalizacji), dodajemy wyznaczony centroid klasy do naszego kontenera i zajmujemy się kolejną klasą problemu (lub kończymy procedurę trenowania i zwracamy klasyfikator).

Predykcja (predict())

Mamy już fit() więc teraz przydałby się i predict(). Zaczynamy od rutyny, czyli sprawdzenia czy model został wcześniej wyuczony oraz czy dane testowe nie są puste i mają odpowiedni kształt.

  def predict(self, X):
        # sprawdzenie do wywolany zostal fit
        check_is_fitted(self)
        # sprawdzenie wejscia
        X = check_array(X)

Dalej postępujemy wedle zasady działania przedstawionej na początku dzisiejszego wpisu. Wyliczamy dystanse każdej instancji testowej do wyznaczonych centroidów klas a następnie wybieramy jako predykcję tą z klas, której centroidu znajdujemy się bliżej. Predykcję oczywiście zwracamy.

        # liczymy dystanse instancji testowych od centroidow
        distance_pred = self.dm_.pairwise(self.centroids_, X)
        # uznajemy, ze instancje naleza do klasy,
        # ktorej centroid znajduje sie blizej
        y_pred = np.argmin(distance_pred, axis=0)
        # zwracamy predykcje
        return y_pred

I to by było na tyle.

Przetestujmy nasz klasyfikator

Wypadałoby przetestować zaimplementowany przez nas model i sprawdzić, czy i jak działa. W tym celu przygotujemy sobie bardzo proste środowisko testowe. Nie dzieje się tutaj nic, z czym nie bylibyśmy już zaznajomieni. Jedyną nowością może być zaimportowanie naszego modelu z wcześniej przygotowanego przez nas pliku z implementacją.

import numpy as np
from onc import OptimizedNearestCentroid
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X, y = make_classification(
    n_samples=700,
    n_features=2,
    n_informative=2,
    n_repeated=0,
    n_redundant=0,
    flip_y=.15,
    random_state=32456,
    n_clusters_per_class=1,
)

X_train, X_test, y_train, y_test = train_test_split(
    X, y,
    test_size=.3,
    random_state=42
)

clf = OptimizedNearestCentroid(optimize=False)
clfo = OptimizedNearestCentroid()
clf.fit(X_train, y_train)
clfo.fit(X_train, y_train)

pred = clf.predict(X_test)
predo = clfo.predict(X_test)

print("Zwykly:         %.3f" % accuracy_score(y_test, pred))
print("Optymalizowany: %.3f" % accuracy_score(y_test, predo))

Spójrzmy na wyniki:

>> Zwykly:         0.914
>> Optymalizowany: 0.924

Faktycznie wygląda na to, że nasza optymalizacja coś robi. Oczywiście jak wiemy, na podstawie tak nienachalnego umysłowo eksperymentu nie możemy wysnuć żadnych wniosków, ale też nie to było dzisiaj naszym celem.

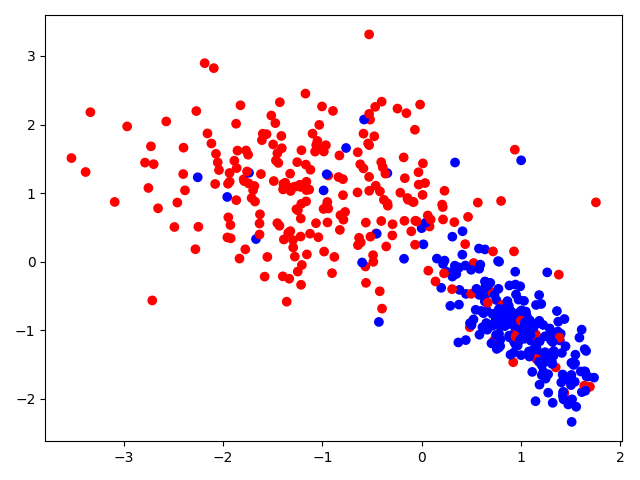
Warto za to spojrzeć na to, jak faktycznie zachowuje się nasz model. W tym celu rzućmy okiem na proste wykresy przestrzeni cech, obrazujące działanie optymalizacji.

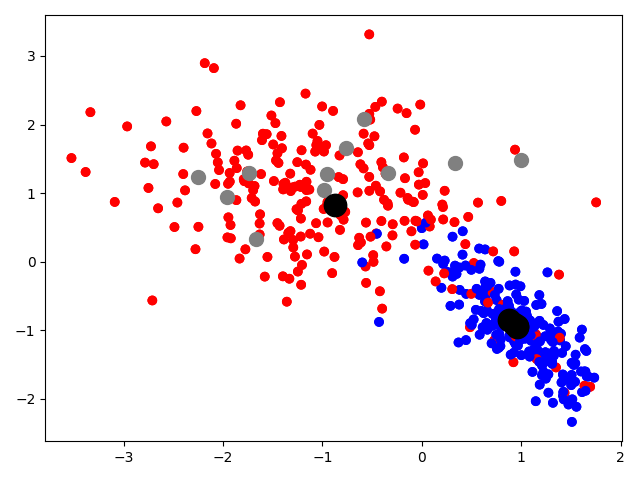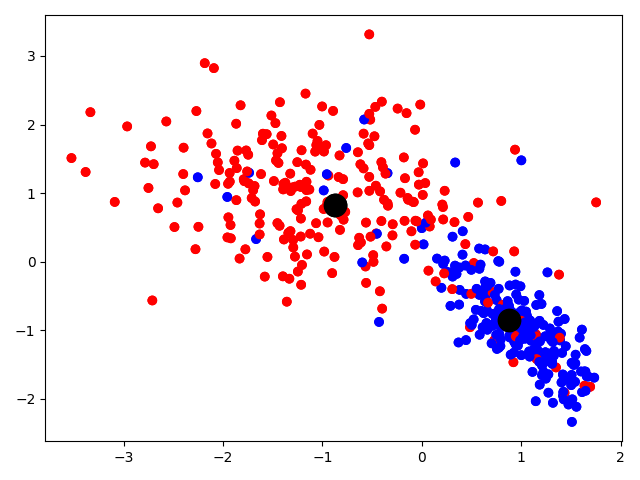
Na pierwszym od lewej wykresie widzimy przestrzeń cech, nie dzieje się tutaj jeszcze nic niesamowitego. Wykres środkowy ukazuje wstępnie wyliczone centroidy klas (oznaczone kolorem czarnym). Magię właściwą możemy zaobserwować na trzecim wykresie – widzimy na nim instancje uznane za obserwacje odstające klasy niebieskiej (oznaczone kolorem szarym) oraz to, jak wraz z ich stopniowym usuwaniem centroid tej klasy przesuwa się na południowy-wschód.

To wszystko na dzisiaj, a za tydzień implementacja własnych klasyfikatorów zespołowych.