Tematem na dzisiaj będzie implementacja zespołu klasyfikatorów. Jest to taki szczególny rodzaj klasyfikatora, który składa się z wielu klasyfikatorów. Zatem przejdźmy od razu do konkretów.
Zespół klasyfikatorów
Na ostatnich zajęciach pokazane było jak napisać implementację klasyfikatora zgodnego z API scikit-learn. Dzisiaj zajmiemy się zespołami klasyfikatorów, inaczej nazywane komitetami klasyfikatorów.
Wstęp
Na początek trochę wyjaśnień. Główna idea budowania zespołów klasyfikatorów oparta jest na tym, że najpierw wiele modeli jest uczonych, a następnie ich predykcje są łączone w celu podjęcia wspólnej decyzji. Zazwyczaj modele te budowane są w oparciu o “proste” klasyfikatory. Wspólne podejmowanie decyzji pozwala uzyskiwanie dobrej jakości klasyfikacji przy zachowaniu odpowiedniej generalizacji. Kluczową tutaj sprawą jest zapewnienie dywersyfikacji komitetu lub inaczej mówiąc różnorodności modeli za pomocą odpowiednich technik. Bezsensowne jest tworzenie zespołu składającego się z klasyfikatorów, które podejmują identyczne decyzje. Dlatego stosuje się odpowiednie metody zapewniające zachowanie różnorodności.
Następnie mając już taki zespół musimy w pewien sposób agregować odpowiedzi wszystkich modeli w jedną wspólną odpowiedź całego komitetu. To w jaki sposób jest to wykonywane określa reguła decyzyjna. Istnieją różne sposoby, jednak najbardziej znanym jest głosowanie twarde. Każdy model wskazuje jakąś etykietę, a większość “głosów” decyduje o tym jaka jest podejmowana decyzja. Jest to dość podobna zasada do koła ratunkowego “Pytanie do publiczności” w popularnym teleturnieju “Milionerzy”. Zakładamy, że wszyscy na publiczności mają równą wagę głosu i każdy typuje jakąś odpowiedź. Wartym wspomnienia jest to, że osoby tam się znajdujące zazwyczaj nie są ekspertami w dziedzinie danego pytania, jednak wspólnymi siłami często potrafią wskazać poprawną odpowiedź na zadane pytanie.
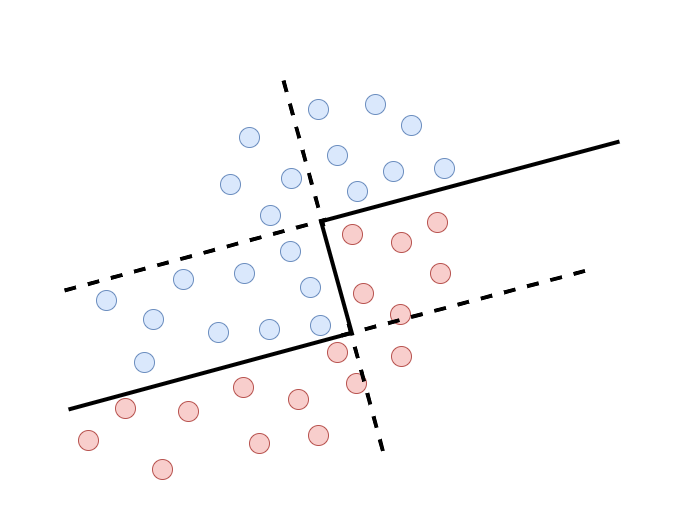
Załóżmy teraz, że mamy pewien problem dwuwymiarowy, który próbujemy rozwiązać za pomocą liniowego klasyfikatora. Jak to jest widoczne na rysunkach poniżej wyznaczenie linii rozdzielającej idealnie dane jest niemożliwe, ponieważ mamy tutaj problem liniowo nieseparowalny. Niebieskie kropki to jedna klasa, a czerwona to druga.
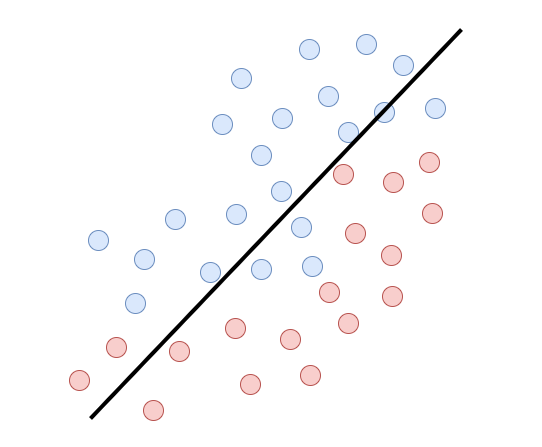
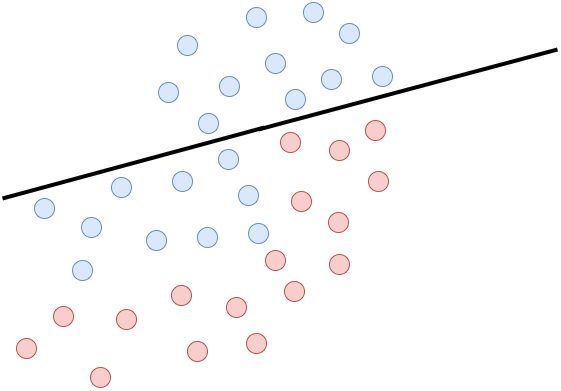
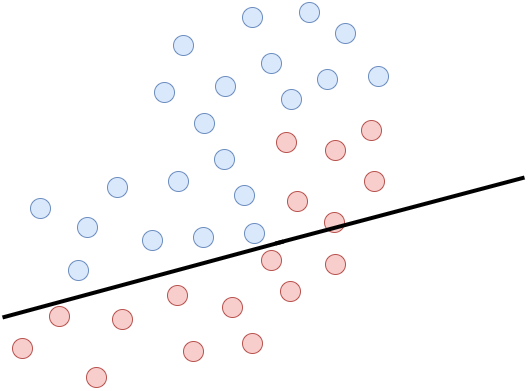
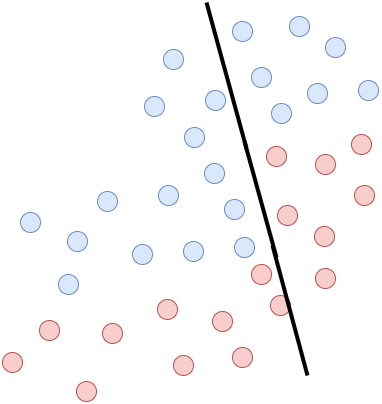
Pojawia się jednak pewne “ale”. Możemy ten problem w miarę skutecznie rozwiązać za pomocą liniowych klasyfikatorów, ale tworząc z nich komitet klasyfikatorów. Kiedy połączymy w odpowiedni sposób trzy modele przedstawione na rysunkach powyżej, otrzymamy zespół klasyfikatorów. Tak wyuczony komitet jest w stanie wyznaczyć granicę decyzyjną opartą na modelach linowych dla problemu liniowo nieseparowalnego. Jak widać na poniższym rysunku jakość predykcji liniowych modeli rośnie, gdy zaczynają działać w jednym zespole. Nie przerywana linia oznacza granicę decyzji dla całego zespołu.
Implementacja
Teraz znając już pewne podstawy, możemy przejść do części implementacyjnej. Stworzenie zespołu to oznacza uczenie wielu modeli, które podejmują wspólną decyzję. Musimy pamiętać o tym, że komitet klasyfikatorów wymaga od nas zapewnienia dywersyfikacji. W tym celu wykorzystamy do tego dość znaną technikę tworzenia losowych podprzestrzeni cech (ang. Random Subspace Ensemble). Oznacza to, że każdy model będzie się uczyć oraz dokonywać predykcji wykorzystując niepełny i losowy zestaw cech danych.
Importy
Na początek stwórzmy sobie nowy plik o nazwie rse.py. W samym nagłówku naszego pliku umieszczamy odpowiednie biblioteki i funkcje potrzebne nam w dalszej części programu. Całość zasadniczo się nie różni jak podczas implementacji klasyfikatora. Jedyny wyjątek to zamiast BaseEstimator, będziemy dziedziczyć klasę BaseEnsemble.
import numpy as np
from sklearn.ensemble import BaseEnsemble
from sklearn.base import ClassifierMixin, clone
from sklearn.utils.validation import check_array, check_is_fitted, check_X_y
Klasa
Kolejny krok to definicja klasy oraz inicjalizator. Parametry jakie będzie przyjmować implementowany zespół to base_estimator, która oznacza klasyfikator jaki będzie używany do tworzenia modeli w komitecie. Maksymalna liczba modeli jest wyrażana za pomocą parametru n_estimators, gdzie wartość domyślna jest równa 10. Parametr n_subspace_features wyraża liczbę wykorzystanych cech do stworzenia jednej podprzestrzeni z wartością domyślną 5. Ilość tych podprzestrzeni jest równa liczbie modeli. Następnie znajduje się parametr ` hard_voting określający jaki jest tryb podejmowania decyzji, domyślnie ustawiony na True. W dalszej części znajdzie się więcej informacji do czego nam ten parametr posłuży. Ostatni to dobrze znany parametr random_state`, który pozwoli na zachowanie pewnej powtarzalności podczas wykonywania eksperymentów.
class RandomSubspaceEnsemble(BaseEnsemble, ClassifierMixin):
"""
Random subspace ensemble
Komitet klasyfikatorow losowych podprzestrzeniach cech
"""
def __init__(self, base_estimator=None, n_estimators=10, n_subspace_features=5, hard_voting=True, random_state=None):
# Klasyfikator bazowy
self.base_estimator = base_estimator
# Liczba klasyfikatorow
self.n_estimators = n_estimators
# Liczba cech w jednej podprzestrzeni
self.n_subspace_features = n_subspace_features
# Tryb podejmowania decyzji
self.hard_voting = hard_voting
# Ustawianie ziarna losowosci
self.random_state = random_state
np.random.seed(self.random_state)
Uczenie
Teraz pora na funkcję, która pozwoli na uczenie całego zespołu. W pierwszej kolejności dokonujemy pewnych rutynowych kroków. Sprawdzenie poprawności danych, zapis nazw klas, dodatkowo zapis liczby atrybutów. Następnie musimy sprawdzić czy liczba cech, które chcemy wykorzystać do tworzenia podprzestrzeni nie jest większa od liczby cech jakie posiadają dane.
def fit(self, X, y):
# Sprawdzenie czy X i y maja wlasciwy ksztalt
X, y = check_X_y(X, y)
# Przehowywanie nazw klas
self.classes_ = np.unique(y)
# Zapis liczby atrybutow
self.n_features = X.shape[1]
# Czy liczba cech w podprzestrzeni jest mniejsza od calkowitej liczby cech
if self.n_subspace_features > self.n_features:
raise ValueError("Number of features in subspace higher than number of features.")
Dopiero teraz przechodzimy do właściwego działania. Losujemy numery indeksów podprzestrzeni cech dla modeli, które będą tworzyć projektowany komitet. Indeksy te musimy zapisać w zmiennej self.subspaces, ponieważ będą później potrzebne podczas predykcji. Następnie tworzymy pusty komitet self.ensembles_ i wypełniamy go modelami wyuczonymi na wcześniej wylosowanych podprzestrzeniach cech. Teraz istotny krok, to użycie do tego metody clone(). Jest to bardzo ważne, aby tworząc nowe modele “klonować” je. Może się zdarzyć sytuacja taka, że bez użycia tej funkcji zespół będzie składać się z wielu, ale niestety identycznych modeli.
# Wylosowanie podprzestrzeni cech
self.subspaces = np.random.randint(0, self.n_features, (self.n_estimators, self.n_subspace_features))
# Wyuczenie nowych modeli i stworzenie zespolu
self.ensemble_ = []
for i in range(self.n_estimators):
self.ensemble_.append(clone(self.base_estimator).fit(X[:, self.subspaces[i]], y))
return self
Predykcja
Podobnie jak na początku uczenia musimy dokonać pewnych kontroli. Po pierwsze sprawdzamy czy nasz komitet jest wyuczony. Takie zabezpieczenie uchroni przed nierozważnymi użytkownikami naszej implementacji, którzy zapragną coś sklasyfikować bez wcześniejszego wyuczenia metody. Następnie kontrola poprawności danych i zgodności liczby cech z danymi użytych do uczenia.
def predict(self, X):
# Sprawdzenie czy modele sa wyuczone
check_is_fitted(self, "classes_")
# Sprawdzenie poprawnosci danych
X = check_array(X)
# Sprawdzenie czy liczba cech się zgadza
if X.shape[1] != self.n_features:
raise ValueError("number of features does not match")
Mając już pewność, że wszystko się zgadza możemy przystąpić do predykcji. W tym miejscu pojawia się wspomniany wcześniej parametr hard_voting. Na samym wstępie został opisany sposób głosowania twardego. Z wykorzystaniem takiej reguły decyzyjnej każdy model wskazuje etykietę dla każdej próbki, a na podstawie większości wskazań podejmowana jest ostateczna predykcja całego zespołu.
Implementacja przebiega w następujący sposób. Na początku tworzona jest pusta lista pred_, które zostaje wypełniona predykcjami poszczególnych modeli. Pamiętamy o tym, że dobieramy odpowiednie podprzestrzenie cech tak samo jak podczas uczenia. Później zamieniana ona jest na macierz typu ndarray z biblioteki numpy. Następnie po dokonaniu transpozycji (pred_.T), predykcje lądują w funkcji pozwalającej na podliczenie maksymalnej liczby etykiet dla poszczególnych próbek. Na sam koniec zwracana jest ostateczna predykcja całego zespołu.
if self.hard_voting:
# Podejmowanie decyzji na podstawie twardego glosowania
pred_ = []
# Modele w zespole dokonuja predykcji
for i, member_clf in enumerate(self.ensemble_):
pred_.append(member_clf.predict(X[:, self.subspaces[i]]))
# Zamiana na miacierz numpy (ndarray)
pred_ = np.array(pred_)
# Liczenie glosow
prediction = np.apply_along_axis(lambda x: np.argmax(np.bincount(x)), axis=1, arr=pred_.T)
# Zwrocenie predykcji calego zespolu
return self.classes_[prediction]
Decyzję można również podejmować za pomocą głosowania miękkiego. Jest to podejście, które również warto poznać. Predykcja jest tutaj oparta na średniej wartości wektorów wsparcia modeli tworzących zespół klasyfikatorów. W pierwszym kroku trzeba pobrać wspomniane wcześniej wektory wsparcia ze wszystkich modeli (funkcja ensemble_support_matrix). Tutaj również musimy pamiętać o tym, że dobieramy odpowiednie podprzestrzenie cech dla modeli. Estymacja wektorów wsparcia określi nam prawdopodobieństwo przynależności klasyfikowanego obiektu do każdej istniejącej klasy. W odpowiedzi (esm) nie uzyskamy więc macierzy etykiet, a macierz wartości zmiennoprzecinkowych. Następnie za pomocą funkcji np.mean obliczamy średnie wsparcie. W kolejnym kroku wskazujemy, która klasa posiada najwyższe prawdopodobieństwo przynależności dla danego obiektu np.argmax, aby na koniec zwrócić uzyskane predykcje.
else:
# Podejmowanie decyzji na podstawie wektorow wsparcia
esm = self.ensemble_support_matrix(X)
# Wyliczenie sredniej wartosci wsparcia
average_support = np.mean(esm, axis=0)
# Wskazanie etykiet
prediction = np.argmax(average_support, axis=1)
# Zwrocenie predykcji calego zespolu
return self.classes_[prediction]
def ensemble_support_matrix(self, X):
# Wyliczenie macierzy wsparcia
probas_ = []
for i, member_clf in enumerate(self.ensemble_):
probas_.append(member_clf.predict_proba(X[:, self.subspaces[i]]))
return np.array(probas_)
Proste eksperymenty
Stworzyliśmy już zespół klasyfikatorów, więc dobrze byłoby sprawdzić czy ta implementacja w ogóle działa. Przeprowadzenie paru bardzo prostych eksperymentów pozwoli nam na szybkie sprawdzenie działania oraz obserwację wpływu niektórych parametrów na jakość predykcji komitetu. Pamiętajmy, że będą to raczej badania uproszczone, co nie pozwali na bezapelacyjne stwierdzenia i wnioski.
Przygotowanie
Na początek importujemy odpowiednie “narzędzia”, które pozwolą na przeprowadzenie prostych testów naszej metody. Klasycznie biblioteka numpy, do tego nowa metoda RandomSubspaceEnsemble. Przydałby się też jakiś bazowy klasyfikator w tym wypadku użyjemy GaussianNB. Aby dodać odrobinę rzetelności naszym testom użyjemy walidacji krzyżowej RepeatedStratifiedKFold, a komitet zmierzymy jak dokładnie działa za pomocą accuracy_score.
import numpy as np
from rse import RandomSubspaceEnsemble
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.metrics import accuracy_score
Wczytujemy wybrany zbiór danych. Tym razem stawiam na dane ze zbioru ionosphere, ale gorąco zachęcam do samodzielnych prób z innymi zbiorami. Jak już dane zostanę wczytane oraz podzielone na cechy i etykiety cenną informacją będzie liczba cech. W tym wypadku są to 34 różne atrybuty.
dataset = 'ionosphere'
dataset = np.genfromtxt("datasets/%s.csv" % (dataset), delimiter=",")
X = dataset[:, :-1]
y = dataset[:, -1].astype(int)
Jak już dane zostanę wczytane oraz podzielone na cechy i etykiety cenną informacją będzie liczba cech. W tym wypadku są to 34 różne atrybuty.
print("Total number of features", X.shape[1])
Następnie musimy przyszykować sobie ustawienia do walidacji krzyżowej. W tym wypadku wystarczą 10 powtórzeń z podziałem 5 części. Pamiętamy o ustawieniu random_state
n_splits = 5
n_repeats = 10
rskf = RepeatedStratifiedKFold(n_splits=n_splits, n_repeats=n_repeats, random_state=1234)
Eksperyment pierwszy
Na początek sprawdźmy jaki wpływ na metodę posiada wybrany tryb podejmowania decyzji - twarde i miękkie głosowanie. W tym celu stworzymy sobie dwa identyczne testy, gdzie jedyną różnicą będzie parametr hard_voting raz ustawiony na wartość True, a w drugim podejściu na wartość False. Wiedząc, że posiadamy 34 cechy spokojnie możemy pozostawić wartość 5 cech na jedną podprzestrzeń. Liczba estymatorów i jednocześnie podprzestrzeni równa 10. Obie te wartości są domyślne.
clf = RandomSubspaceEnsemble(base_estimator=GaussianNB(), n_estimators=10, n_subspace_features=5, hard_voting=True, random_state=123)
scores = []
for train, test in rskf.split(X, y):
clf.fit(X[train], y[train])
y_pred = clf.predict(X[test])
scores.append(accuracy_score(y[test], y_pred))
print("Hard voting - accuracy score: %.3f (%.3f)" % (np.mean(scores), np.std(scores)))
clf = RandomSubspaceEnsemble(base_estimator=GaussianNB(), n_estimators=10, n_subspace_features=5, hard_voting=False, random_state=123)
scores = []
for train, test in rskf.split(X, y):
clf.fit(X[train], y[train])
y_pred = clf.predict(X[test])
scores.append(accuracy_score(y[test], y_pred))
print("Soft voting - accuracy score: %.3f (%.3f)" % (np.mean(scores), np.std(scores)))
Uzyskane wyniki wskazują, że średnia dokładność predykcji podczas tego testu jest lepsza dla głosowania miękkiego. Głosowanie twarde wykazuje mniejsze odchylenie standardowe.
Hard voting - accuracy score: 0.800 (0.045)
Soft voting - accuracy score: 0.823 (0.053)
Eksperyment drugi
Kolejna właściwość jaką można sprawdzić to wpływ liczby cech użytej do stworzenia jednej podprzestrzeni. W tym wypadku przetestowana zostaną przetestowane trzy różne wartości 10, 15 i 20 cech.
clf = RandomSubspaceEnsemble(base_estimator=GaussianNB(), n_estimators=10, n_subspace_features=10, hard_voting=False, random_state=123)
scores = []
for train, test in rskf.split(X, y):
clf.fit(X[train], y[train])
y_pred = clf.predict(X[test])
scores.append(accuracy_score(y[test], y_pred))
print("10/34 features - accuracy score: %.3f (%.3f)" % (np.mean(scores), np.std(scores)))
clf = RandomSubspaceEnsemble(base_estimator=GaussianNB(), n_estimators=10, n_subspace_features=15, hard_voting=False, random_state=123)
scores = []
for train, test in rskf.split(X, y):
clf.fit(X[train], y[train])
y_pred = clf.predict(X[test])
scores.append(accuracy_score(y[test], y_pred))
print("15/34 features - accuracy score: %.3f (%.3f)" % (np.mean(scores), np.std(scores)))
clf = RandomSubspaceEnsemble(base_estimator=GaussianNB(), n_estimators=10, n_subspace_features=20, hard_voting=False, random_state=123)
scores = []
for train, test in rskf.split(X, y):
clf.fit(X[train], y[train])
y_pred = clf.predict(X[test])
scores.append(accuracy_score(y[test], y_pred))
print("20/34 features - accuracy score: %.3f (%.3f)" % (np.mean(scores), np.std(scores)))
Wyniki pokazują, że najlepszy wynik uzyskuje liczba 15 cech.
10/34 features - accuracy score: 0.830 (0.050)
15/34 features - accuracy score: 0.855 (0.045)
20/34 features - accuracy score: 0.851 (0.047)
Eksperyment trzeci
Ostatni eksperyment ma na celu sprawdzenie doboru liczby klasyfikatorów, tworzących jeden zespół. W tym teście zostały wybrane wartości 5, 10 i 15.
clf = RandomSubspaceEnsemble(base_estimator=GaussianNB(), n_estimators=5, n_subspace_features=15, hard_voting=False, random_state=123)
scores = []
for train, test in rskf.split(X, y):
clf.fit(X[train], y[train])
y_pred = clf.predict(X[test])
scores.append(accuracy_score(y[test], y_pred))
print("5 estimators - accuracy score: %.3f (%.3f)" % (np.mean(scores), np.std(scores)))
clf = RandomSubspaceEnsemble(base_estimator=GaussianNB(), n_estimators=10, n_subspace_features=15, hard_voting=False, random_state=123)
scores = []
for train, test in rskf.split(X, y):
clf.fit(X[train], y[train])
y_pred = clf.predict(X[test])
scores.append(accuracy_score(y[test], y_pred))
print("10 estimators - accuracy score: %.3f (%.3f)" % (np.mean(scores), np.std(scores)))
clf = RandomSubspaceEnsemble(base_estimator=GaussianNB(), n_estimators=15, n_subspace_features=15, hard_voting=False, random_state=123)
scores = []
for train, test in rskf.split(X, y):
clf.fit(X[train], y[train])
y_pred = clf.predict(X[test])
scores.append(accuracy_score(y[test], y_pred))
print("15 estimators - accuracy score: %.3f (%.3f)" % (np.mean(scores), np.std(scores)))
Wyniki pokazują, że najlepsze rezultaty metoda uzyskuje posiadając 10 modeli tworzących zespół.
5 estimators - accuracy score: 0.840 (0.051)
10 estimators - accuracy score: 0.855 (0.045)
15 estimators - accuracy score: 0.854 (0.041)
Wnioski
Z przeprowadzonych badań można wyciągnąć parę ciekawych wniosków. Po pierwsze widać, że zaprojektowany zespół posiada parametry, które znacząco wpływają na jakość działania. Dobór odpowiednich wartości parametrów, może okazać się kluczowy podczas wykorzystywania tej metody. Kolejny wniosek jaki się nasuwa to, że nie zawsze więcej oznacza lepiej. Zauważalne jest to, że większa liczba estymatorów lub cech w podprzestrzeni nie zawsze daje polepszenie dokładności. Tutaj trzeba raczej szukać wartości wyważonej, niekoniecznie bardzo dużej. Nie było to sprawdzane, ale można się domyślać, że większa liczba estymatorów lub cech w podprzestrzeni może się wiązać z większym obciążeniem procesora, a co za tym idzie wydłużonym czasem działania. Pamiętajmy jednak, że są to tylko pewne hipotezy, które wymagają szerszego przebadania w celu uzyskania potwierdzenia.
To by było na tyle dzisiaj. Gorąco namawiam do “zabawy” z użyciem zaprezentowanej tu implementacji zespołu klasyfikatorów opartego na losowych podprzestrzeniach cech. Może jakiś własny pomysł na dywersyfikację zespołu lub ciekawy test tego zespołu. Może wyjdą inne wyniki, może dla innych danych lub jakiś własnych eksperymentów. Może nasunął się jakieś nowe wnioski, czy powstaną modyfikacje tego kodu. Wszystkie osoby, którym uda się coś napisać lub zrobić, ogromnie zachęcam do podzielenia się swoimi implementacjami lub wnioskami mailowo. Czekam z wielką niecierpliwością!
jakub.klikowski@pwr.edu.pl