Przykłady 8 — Klasyfikacja niezbalansowanych danych (binarnych)

“Balance. It was all about balance. That had been one of the first things that she had learned […]”
― Terry Pratchett, I Shall Wear Midnight

Dane niezbalansowane

Problem nazywamy niezbalansowanym, kiedy (w przypadku binarnym) mamy do czynienia z dwoma klasami, z których liczność jednej (większościowej) znacząco przewyższa liczność drugiej (mniejszościowej). Przykład takiego problemu możemy zobaczyć na poniższym rysunku, który obrazuje w przestrzeni cech 200 instancji, z których 95% należy do klasy większościowej (niebieskiej), a 5% do klasy mniejszościowej (czerwonej):

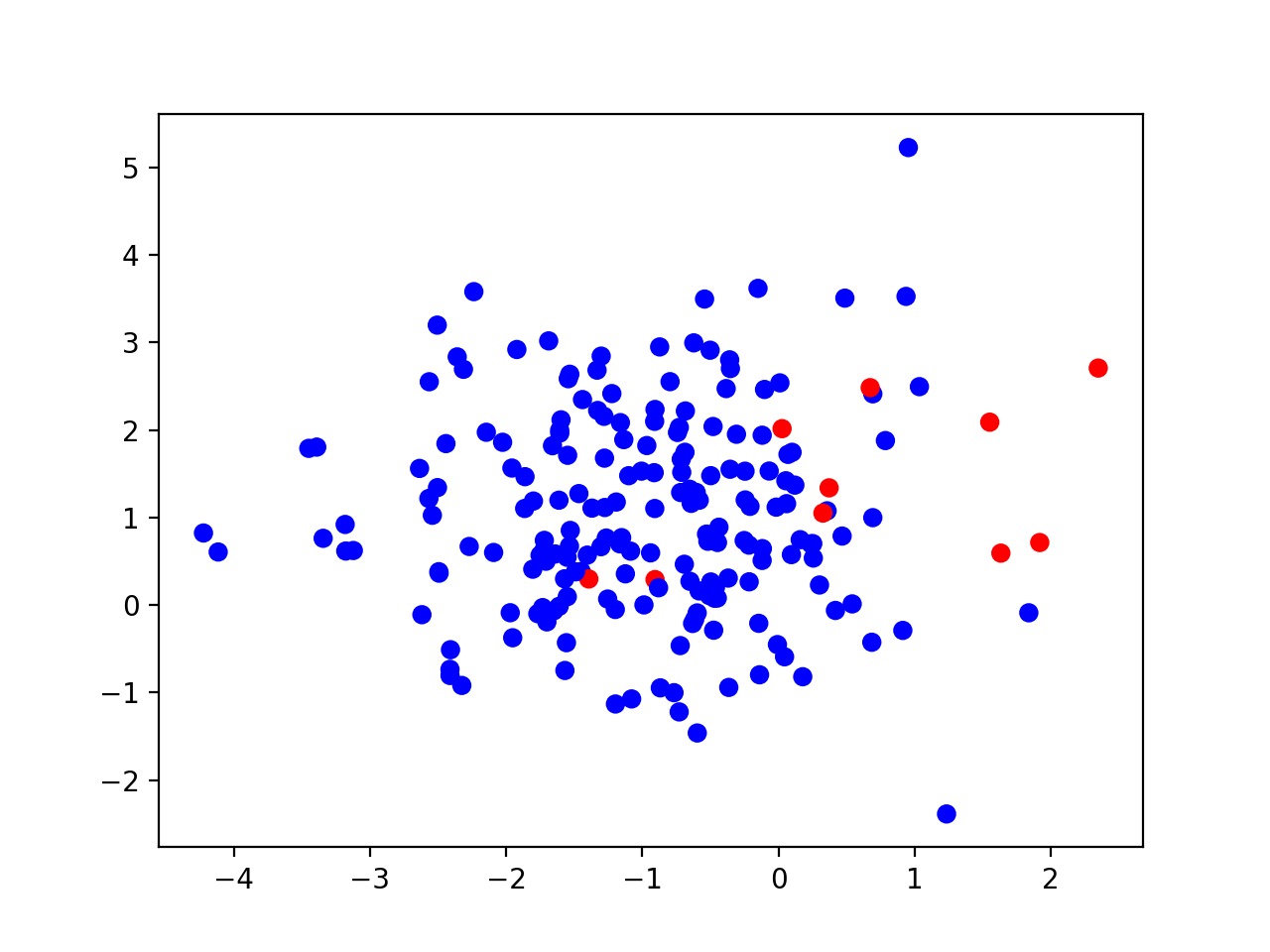
Taka sytuacja stanowi dla nas problem, ponieważ zdecydowana większość tradycyjnych algorytmów uczenia maszynowego – wytrenowanych na takim zbiorze – posiada bias w stosunku do klasy większościowej (preferuje tą klasę) w procesie predykcji. A równocześnie tak się składa, że zazwyczaj to poprawne rozpoznanie instancji klasy mniejszościowej jest dla nas ważniejsze.

Dodatkowo, w przypadku problemów niezbalansowanych, nie możemy stosować jakości klasyfikacji jako metryki ewaluacji naszych algorytmów. Wystarczy spojrzeć na powyższy przykład i zastanowić się, jaka byłaby jakość klasyfikacji, gdybyśmy po prostu uznawali każdą instancję problemu za należącą do klasy większościowej. Otrzymalibyśmy wtedy model dający nam ~95% jakości klasyfikacji (czyli teoretycznie bardzo dobry), ale jednocześnie nie rozpoznalibyśmy żadnej instancji klasy mniejszościowej. Dlatego właśnie potrzebujemy metryk, które dostarczają nam więcej informacji, niż tylko % poprawnie zaklasyfikowanych próbek.

Zapoznajmy się więc z istniejącymi podejściami do radzenia sobie z niezbalansowaniem oraz z metrykami, które pozwolą nam w sensowny sposób ocenić w takim przypadku działanie modelu.

Podejścia do radzenia sobie z niezbalansowaniem

Możemy wyróżnić trzy główne podejścia do uczenia się z danych niezbalansowanych [Krawczyk2016]:

Na poziomie danych (ang. Data-level methods), które modyfikują dostępne instancje problemu w celu jego zbalansowania. Tutaj najbardziej popularne podejścia to (i) oversampling, który generuje sztuczne instancje klasy mniejszościowej oraz (ii) undersampling, który pozbywa się instancji klasy większościowej.
Na poziomie algorytmów (ang. Algorithm-level methods), które modyfikują istniejące algorytmy uczenia maszynowego, aby zredukować ich bias w kierunku klasy większościowej.
Podejścia hybrydowe (ang. Hybrid methods), łączące oba wyżej opisane rozwiązania.

My dzisiaj zajmiemy się podejściami na poziomie danych, a więc oversamplingiem i undersamplingiem. Wybierzemy w tym celu po dwie metody z każdej grupy:

Oversampling
- Random Oversampling (ROS) - najprostsza koncepcyjnie metoda oversamplingu, która wyrównuje liczność klas poprzez powielanie istniejących instancji klasy mniejszościowej (poprzez losowanie ze zwracaniem).
- Synthetic minority over-sampling technique (SMOTE) - klasyczny algorytm oversamplingu, który generuje syntetyczne instancje klasy mniejszościowej pomiędzy istniejącymi instancjami tej klasy a ich sąsiadami (również z klasy mniejszościowej).
Udersampling
- Random Undersampling (RUS) - adekwatnie do ROS, tylko w drugą stronę - usuwamy losowe instancje klasy większościowej aż nie zbalansujemy problemu. Niestety, możemy przez to stracić przydatne informacje.
- Condensed Nearest Neighbour (CNN) - technika undersamplingu, która usuwa te instancje klasy większościowej, które można poprawnie zaklasyfikować korzystając z 1-NN (Algorytmu najbliższych sąsiadów z jednym sąsiadem). Dzięki temu zostawiamy instancje klasy większościowej, które znajdują się blisko granicy decyzyjnej.

Ewaluacja w przypadku niezbalansowanych problemów (binarnych)

Czas na metryki, którymi posługujemy się, gdy mamy do czynienia z problemami niezbalansowanymi. Dzisiaj poznamy sześć metryk. Definicje trzech z nich wynikają bezpośrednio z dobrze nam znanej macierzy konfuzji, metryki te nazywamy bazowymi. Pozostałe trzy metryki (metryki zagregowane), składają się z metryk bazowych. Koncentrujemy się dzisiaj wyłącznie na problemach binarnych, problemy wieloklasowe wymagają bardziej skomplikowanej formy prezentacji wyników.

Metryki bazowe

Zacznijmy od macierzy konfuzji, tak dla przypomnienia:

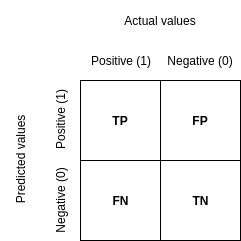
Musimy także pamiętać, że aby poniższe metryki były informatywne, klasa mniejszościowa musi być pozytywna.

Sensitivity (Recall)

Recall mówi nam o tym, jak dobrze nasz algorytm radzi sobie z rozpoznawaniem obiektów klasy mniejszościowej. Dzięki niemu wiemy, ile obiektów uznaliśmy za należące do klasy mniejszościowej w stosunku do tego, ile faktycznie ich jest.

$Recall = \frac{tp}{tp + fn}$

Precision

Precision informuje nas o tym, jak dokładny jest nasz algorytm podczas rozpoznawania klasy mniejszościowej. Dzięki temu wiemy, ile z obiektów, które przyporządkowaliśmy do tej klasy, faktycznie do niej należy.

$Precision = \frac{tp}{tp + fp}$

Specificity

Specificity działa jak recall, ale dla klasy większościowej.

$Specificity = \frac{tn}{tn + fp}$

Metryki zagregowane

F1-score

F1 score, a dokładniej Fβ score, gdzie β wynosi 1. Jest to średnia harmoniczna precision i recall.

$F_1 = 2 * \frac{Precision * Recall}{Precision + Recall}$

Geometric mean score (G-mean)

G-mean, przynajmniej w tej wersji (istnieje jeszcze druga, ale ona raczej nie jest nam potrzebna), stanowi pierwiastek iloczynu recall i precision.

$Gmean = \sqrt{Recall * Specificity}$

Balanced accuracy (BAC)

Zbalansowana dokładność to po prostu średnia recall i specificity.

$BAC = \frac{Recall + Specificity}{2}$

Eksperyment

Spróbujmy wykorzystać przedstawioną poniżej wiedzę w praktyce. Czas na mały eksperyment.

Wczytanie danych, bez komentarza:

# wczytanie zestawu danych
import numpy as np

dataset = 'ecoli-0-1-4-6_vs_5'
dataset = np.genfromtxt("%s.csv" % (dataset), delimiter=",")
X = dataset[:, :-1]
y = dataset[:, -1].astype(int)

Teraz zdefiniujemy sobie wykorzystywany klasyfikator (drzewo decyzyjne CART), a także wcześniej opisane metody preprocessingu i metryki. Metody preprocessingu pochodzą z biblioteki imbalanced-learn, natomiast metryki importowane są ze stream-learn.

# zdefiniowanie klasyfikatorów, technik preprocessingu i metryk
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from imblearn.over_sampling import RandomOverSampler, SMOTE
from imblearn.under_sampling import RandomUnderSampler, CondensedNearestNeighbour
from strlearn.metrics import recall, precision, specificity, f1_score,
geometric_mean_score_1, balanced_accuracy_score

clf = DecisionTreeClassifier(random_state=1410)
preprocs = {
    'none': None,
    'ros': RandomOverSampler(random_state=1410),
    'smote' : SMOTE(random_state=1410),
    'rus': RandomUnderSampler(random_state=1410),
    'cnn': CondensedNearestNeighbour(random_state=1410),
}
metrics = {
    "recall": recall,
    'precision': precision,
    'specificity': specificity,
    'f1': f1_score,
    'g-mean': geometric_mean_score_1,
    'bac': balanced_accuracy_score,
}

I na koniec standardowa walidacja krzyżowa, z tym, że wyniki przechowujemy w macierzy o trzech wymiarach (metoda preprocessingu, fold, metryka). Preprocessingu dokonujemy za pomocą funkcji fit_resample().

# walidacja krzyżowa
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.base import clone

n_splits = 5
n_repeats = 2
rskf = RepeatedStratifiedKFold(
    n_splits=n_splits, n_repeats=n_repeats, random_state=42)

scores = np.zeros((len(preprocs), n_splits * n_repeats, len(metrics)))

for fold_id, (train, test) in enumerate(rskf.split(X, y)):
    for preproc_id, preproc in enumerate(preprocs):
        clf = clone(clf)

        if preprocs[preproc] == None:
            X_train, y_train = X[train], y[train]
        else:
            X_train, y_train = preprocs[preproc].fit_resample(
                X[train], y[train])

        clf.fit(X_train, y_train)
        y_pred = clf.predict(X[test])

        for metric_id, metric in enumerate(metrics):
            scores[preproc_id, fold_id, metric_id] = metrics[metric](
                y[test], y_pred)

# Zapisanie wynikow
np.save('results', scores)

Prezentacja rezultatów

Jako, że korzystaliśmy z sześciu metryk, to dobrym pomysłem na przeanalizowanie uzyskanych wyników jest odpowiedni wykres. Jako, że osobiście jestem fanem wykresów radarowych, to taki właśnie narysujemy. Poniżej kod, który powstał w oparciu o ten przykład.

Wczytujemy zapisane wyniki i uśredniamy je po drugim wymiarze (czyli po foldach) oraz transponujemy:

import numpy as np
import matplotlib.pyplot as plt
from math import pi

scores = np.load("results.npy")
scores = np.mean(scores, axis=1).T

Przygotowujemy listę metryk i metod oraz rysujemy ‘tło’ naszego wykresu:

# metryki i metody
metrics=["Recall", 'Precision', 'Specificity', 'F1', 'G-mean', 'BAC']
methods=["None", 'ROS', 'SMOTE', 'RUS', 'CNN']
N = scores.shape[0]

# kat dla kazdej z osi
angles = [n / float(N) * 2 * pi for n in range(N)]
angles += angles[:1]

# spider plot
ax = plt.subplot(111, polar=True)

# pierwsza os na gorze
ax.set_theta_offset(pi / 2)
ax.set_theta_direction(-1)

# po jednej osi na metryke
plt.xticks(angles[:-1], metrics)

# os y
ax.set_rlabel_position(0)
plt.yticks([0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1],
["0.0","0.1","0.2","0.3","0.4","0.5","0.6","0.7","0.8","0.9","1.0"],
color="grey", size=7)
plt.ylim(0,1)

Rysujemy na wykresie wyniki dla każdej z testowanych metod preprocessingu, dodajemy legendę i zapisujemy wykres:

# Dodajemy wlasciwe ploty dla kazdej z metod
for method_id, method in enumerate(methods):
    values=scores[:, method_id].tolist()
    values += values[:1]
    print(values)
    ax.plot(angles, values, linewidth=1, linestyle='solid', label=method)

# Dodajemy legende
plt.legend(bbox_to_anchor=(1.15, -0.05), ncol=5)
# Zapisujemy wykres
plt.savefig("radar", dpi=200)

Naszym oczom ukazuje się taka oto radość:

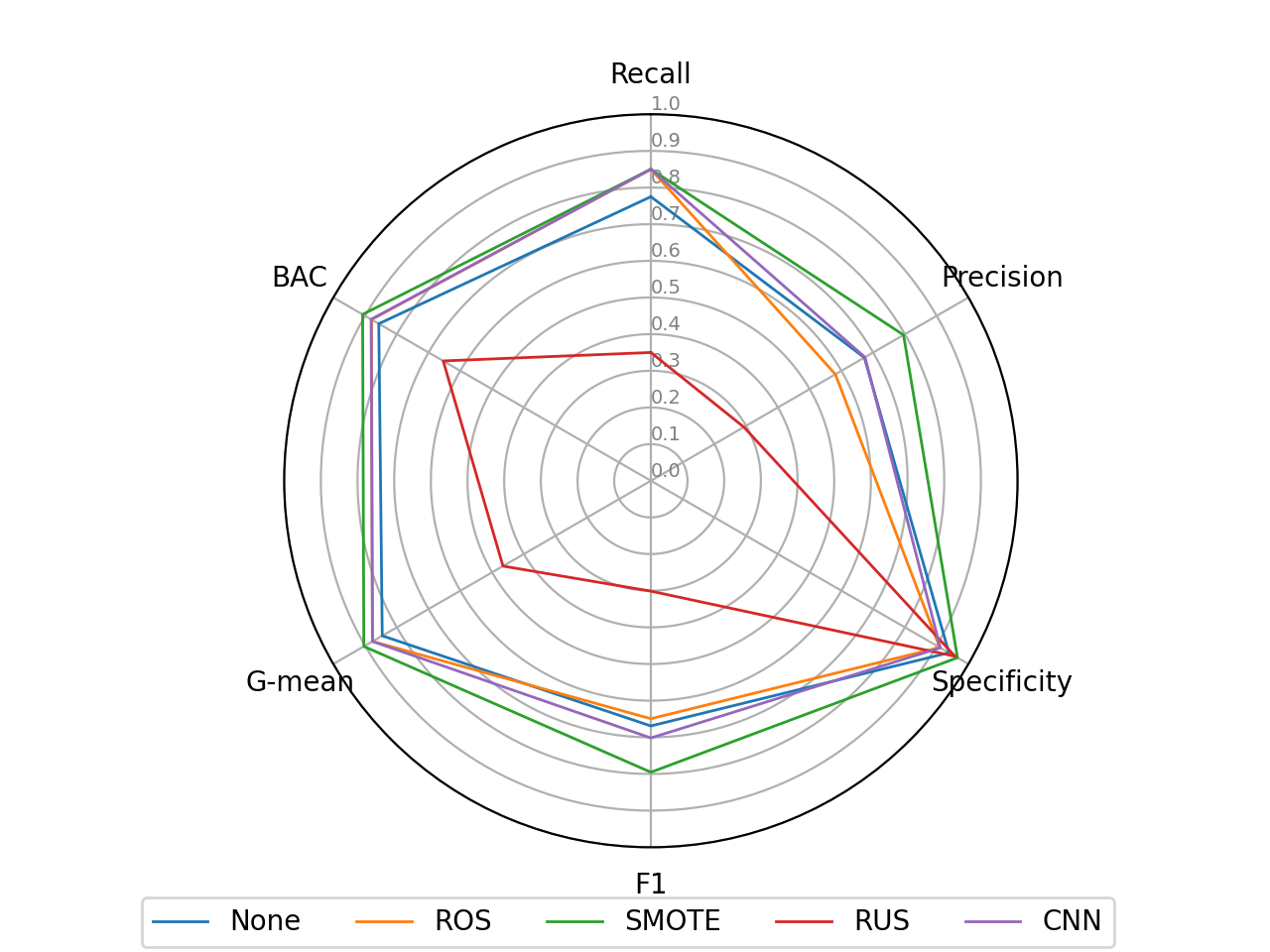
Oczywiście jest on bardzo podstawowy i przy odrobinie chęci moglibyśmy sprawić, aby był o wiele bardziej czytelny. Jednak zamiast tego, skoncentrujmy się na uzyskanych wynikach.

Jak widzimy, zdecydowanie najgorzej spisał się RUS, co najprawdopodobniej jest związane z pozbyciem się przez algorytm instancji niosących ze sobą ważne informacje. ROS poprawił zdolność drzewa decyzyjnego do wykrywania klasy mniejszościowej, jednak przypłacił to spadkiem precyzji (jest to bardzo często zjawisko, tak samo, jak zwiększanie precyzji kosztem recallu). CNN, dzięki usuwaniu tylko obiektów położonych daleko od granicy decyzyjnej, poprawił recall bez pogorszenia precyzji - jednak osłabił nieznacznie specificity. Zdecydowanie najlepiej spisał się SMOTE, który doprowadził do poprawy pod względem wszystkich sześciu analizowanych metryk.

Oczywiście, aby badania były pełne, potrzebowalibyśmy większej liczby zestawów danych oraz odpowiednich testów statystycznych. Jednak nie to było przedmiotem dzisiejszych przykładów.

To już wszystko z mojej strony. Za tydzień mgr Klikowski przedstawi, w ostatnich już przykładach, w jaki sposób przeprowadzamy badania na strumieniach danych.